模拟退火算法
简介
由于很多题的正解可能会有一点困难,而整个题的大致内容又可以抽象为找出某一个函数的最大/最小值时,就可以试着用模拟退火来解决。
假设有如下一段函数:
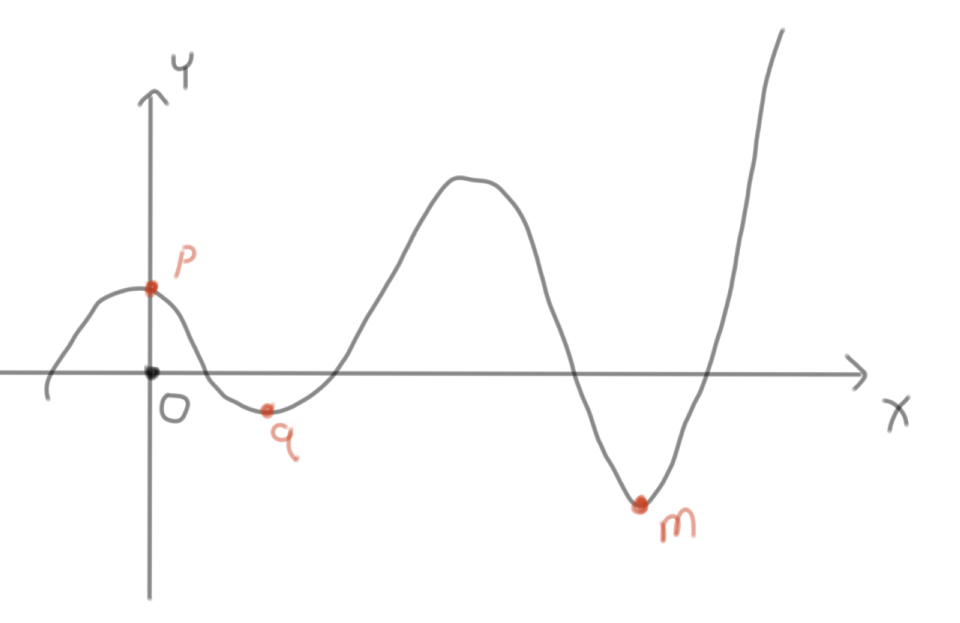
从O点出发,贪心的去查找函数的最低点,最终会陷入q点这个局部最优解而无法跳出去。而真正的最优解实际上是m点。
联系到物理上退火降温的过程,一个处于很高温度的物体,现在要给它降温,使物体内能降到最低。常规的思维就是让温度直接迅速降低,但实际上,过快地降温会使得物体来不及有序地收缩,难以形成内能最低的结晶态。正确的做法是徐徐降温,才能使得物体的每一个粒子都有足够的时间找到自己的最佳位置并紧密有序地排列。开始温度高的时候,粒子活跃地运动并逐渐找到一个合适的状态。在这过程中温度也会越降越低,温度低下来了,那么粒子也渐渐稳定下来,相较于以前不那么活跃了。这时候就可以慢慢形成最终稳定的结晶态了。(这一段话参考自大佬FlashHu的博客)
针对于上面那个函数图,在陷入q这个局部最优解时,我们让它以一定的概率去接受并不优于它的解,这样才能跳出局部的限制。而这个概率就是e^(△f/T)。T是当前温度,△f是当前点的函数值f(x)与目标点函数值f(x+△x)的变化量。而关于x怎么跳,我们可以初始选定一个点x,然后让△x在一个大小与T成正比的值域内随机取值来模拟变动的大小随温度的降低而降低。当反复执行这个过程,使得T从一个很高的值降到给定的EPS(足够趋近于0)时,可以认为此时的最优解就是全局最优解。
(模拟退火的调参过程可能比较漫长,比如温度变化量△T一般取0.95-0.99,一开始可以尽可能的把计算量拉满,先跑出来答案,再去优化参数。并且可以让程序进行多次模拟退火,以确保答案的准确性。)
下面是一些例题:
[JSOI2004]平衡点
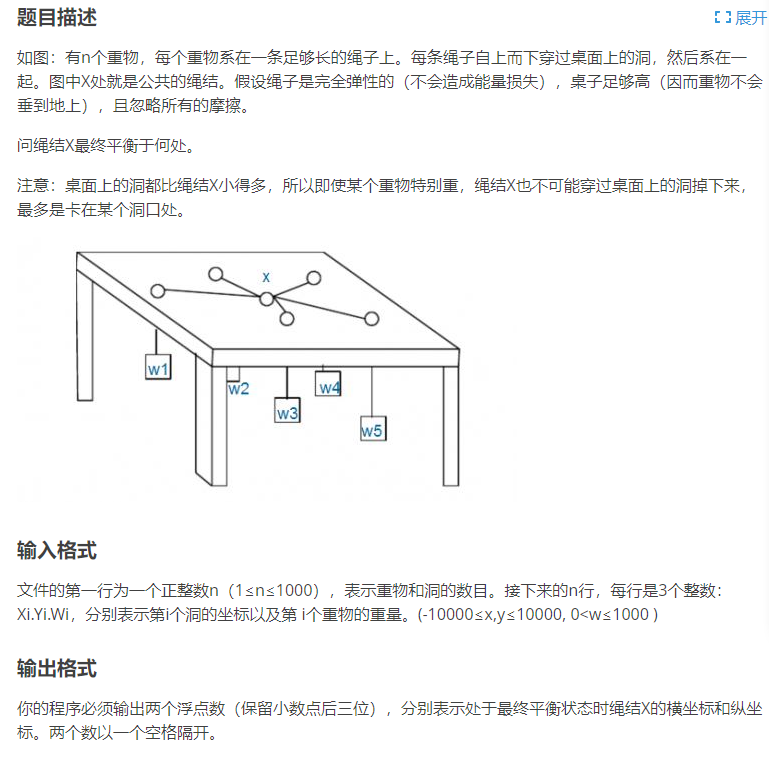
分析题目得知,绳结平衡下来时,各物体的能量之和达到了最低状态,对于这道题也就是让重力势能之和最低。物体的势能之和要最低,其实就是让每个物体桌面上那一段绳子的长度尽可能短。因而,每一个物体的势能都和它在桌子上那一段绳子的长度以及它的重量成正比。所以我们可以用模拟退火来找出这个最低状态的坐标点,将绳结的位置作为自变量,物体势能之和作为因变量,找出函数最低点。
//#define LOCAL
//#pragma gcc optimize(2)
#include <iostream>
#include <iomanip>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <vector>
#include <queue>
#include <algorithm>
#include <map>
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sp(a) fixed<<setprecision(a)
#define INF 0x3f3f3f3f
#define PI acos(-1)
#define per(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ps(a) printf("%s", a)
#define pi(a) printf("%d\n", a)
#define pl(a) printf("%lld\n", a)
#define pu(a) printf("%llu\n", a)
#define sc(a) scanf("%d", &a)
#define scl(a) scanf("%lld", &a)
#define lowbit(a) (a & -a)
#define debug(a) pi(a)
#define CC getchar(), getchar()
#define br ps("\n")
#define endl "\n"
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N = 1e3 + 5;
const double DK = 0.99, EPS = 1e-14; //温度变化率和EPS
double w[N], x[N], y[N];
int n, T = 10;
double calc(double x0, double y0){
long double ret = 0;
per(i,1,n){
double dx = x[i]-x0, dy = y[i]-y0;
ret += sqrt(dx*dx+dy*dy)*w[i];
}
return ret;
}
int main(){
srand((unsigned)time(NULL));
double sum_x = 0, sum_y = 0, ans_x, ans_y, best, glo_best, base_x, base_y, cur;
cin>>n;
per(i,1,n){
cin>>x[i]>>y[i]>>w[i];
sum_x += x[i], sum_y += y[i];
}
ans_x = sum_x/n, ans_y = sum_y/n; //选取的初始绳结坐标
glo_best = calc(ans_x, ans_y);
while(T--){ //这里也可以写成(clock()<CLOCKS_PER_SECOND*0.9)来卡时间
best = glo_best, base_x = ans_x, base_y = ans_y;
for(double k = 50000;k>EPS;k*=DK){
//[-k*RAND_MAX, k*RAND_MAX)
double cur_x = base_x + k*(rand()*2-RAND_MAX);
double cur_y = base_y + k*(rand()*2-RAND_MAX);
cur = calc(cur_x, cur_y);
if(cur<glo_best){ //这种情况直接接受
glo_best = cur, ans_x = cur_x, ans_y = cur_y;
}
//一定概率来接受
if(cur<best || exp((best-cur)/k)>(double)rand()/RAND_MAX){
best = cur, base_x = cur_x, base_y = cur_y;
}
}
}
cout<<sp(3)<<ans_x<<" "<<ans_y<<endl;
return 0;
}